دلیل علاقه ریاضی‌دان‌ها به بریدن کیک چیست؟

به گزارش اقتصادنیوز به نقل از زومیت، آریل پروکاچیا در طی پانزده سال گذشته، به روش‌های مختلفی درباره‌ی چگونگی برش یک کیک فکر کرده است. دلیلش هم این است که این دانشمند کامپیوتر هاروارد سه فرزند دارد که در طی سال‌های گذشته برایشان چندین جشن تولد گرفته است. او می‌داند ایستادن با یک چاقو در مقابل یک شاهکار چندلایه چه حسی دارد.

پاسخ به پرسش فوق فراتر از یک جشن تولد ساده است. به نوشته‌ی ساینس نیوز، تأمل درباره‌ی بریدن کیک در واقع به زیرشاخه‌ای وسیع از ریاضی ربط دارد که هدف آن تقسیم عادلانه‌ی منابع است. این مسئله زمینه‌ساز الگوریتم‌هایی شد که به تخصیص غذا در میان جوامع گرسنه، چگونگی تقسیم اجاره‌خانه یا کارهای روزمره در میان هم‌اتاقی‌ها، چگونگی کشیدن مرز برای رسیدن به مناطق عادلانه‌ی رأی‌گیری و بسیاری از موارد دیگر ربط دارند.

کیک استعاره‌ای از هر گونه کالای تقسیم‌پذیر و منابع محدود است

مسئله‌ی برش کیک در واقع یک استنتاج بسیار دقیق را به پرسش‌هایی درباره‌ی اولویت‌های انسان و مسائل جهان واقعی ربط می‌دهد، به‌طوری که نه تنها ریاضی‌دان‌ها بلکه دانشمندان کامپیوتر، اقتصاددان‌ها، دانشمندان اجتماعی و کارشناسان حقوقی را هم به خود جذب می‌کند. پرسش‌های برابری یا نابرابری معمولا به صورت جهانی مطرح می‌شوند. به گفته‌ی پروکاچیا، از مدل برش کیک می‌توان به مفهوم انصاف رسید و درباره‌ی آن استدلال کرد.

به گفته استیون برامز، نظریه‌پرداز بازی و دانشمند علوم سیاسی دانشگاه نیویورک، کیک در واقع استعاره‌ای برای هر کالای تقسیم‌پذیر مثل زمین، زمان یا به طور کلی منابع محدود است. وقتی دیدگاه‌های مرتبط با برش کیک را روی مسائل بین‌المللی پیاده‌سازی کنیم، می‌توانیم راه‌حل بسیاری از مشکلات را به دنیا ارائه دهیم.

کارشناس‌ها همچنین بارها و به شکل‌های مختلف الگوریتم‌ها یا قوانین ریاضی را برای برش عادلانه کیک ارائه داده‌اند. این روش‌ها اغلب اوقات متمرکز بر کیک‌های مستطیلی هستند. با این‌حال مسئله‌ی جدید برش پای بر دسرهای دایره‌ای یا پیتزا تأکید دارد. ساده‌ترین قوانین نشان می‌دهند چگونه یک کیک را به صورت عادلانه بین دو نفر تقسیم کنید: شخصی کیک را به دو قسمت تقسیم می‌کند که تصور می‌کند از لحاظ ابعاد برابر هستند و شخص دیگر قطعه‌ی اول را برمی‌دارد. هر شخص بخشی از کیک را دریافت می‌کند که به باور او به اندازه‌ی برش طرف مقابل ارزشمند است. قدمت گزارش‌های تقسیم عادلانه به یونان باستان بازمی‌گردد.

در دهه‌ی ۱۹۴۰ میلادی، ریاضیدان‌ها به صورت جدی به روش‌های تقسیم عادلانه‌ی کیک علاقه نشان دادند. آن‌ها چگونگی تقسیم عادلانه در میان سه نفر را بررسی کردند. این دیدگاه به توسعه‌ی الگوریتم‌ها به تعداد دلخواه افراد و پرسش‌های پیچیده‌تری مثل برابری چیست و چگونه آن را ثابت می‌کنید، انجامید.

پژوهشگرها در سال‌های گذشته در زمینه‌ی شناسایی کمترین تعداد برش لازم برای تعداد مشخصی از افراد و همچنین حداکثر تعداد برش‌ها به پیشرفت‌هایی رسیده‌اند. با اینکه تعداد برش‌ها می‌توانند بسیار زیاد باشند، تمام راه‌حل‌ها نشان داده‌اند این مسئله متناهی است. همچنان تغییرات جدیدی روی مسئله اعمال می‌شوند.

برای مثال، اگر به جای تک تک افراد، کیکی را برای گروه‌های چندتایی از افراد برش بزنید چه اتفاقی رخ می‌دهد؟ یا اگر گیرندگان کیک درباره‌ی اولویت‌های خود دروغ بگویند چه نتیجه‌ای به دست می‌آید؟ یا اگر نتیجه‌ی تقسیم گسسته باشد، چطور؟ ریاضیدان‌ها با تمرکز بر تعریف‌های دقیق و سناریوهای جدید، کاربردهای جدیدی را پیدا کردند و مسئله‌ی برش کیک را در خط مقدم پژوهش‌های برابری قرار دادند.

دستورالعمل‌هایی برای برش عادلانه کیک

آزمایش‌های مستند و جستجوی روش‌های عادلانه برای تقسیم، به شعری از هسیود با عنوان تئوگونیا بازمی‌گردد که حدود ۲۷۰۰ سال پیش به نگارش درآمد. بر اساس یکی از داستان‌ها، خدایان و فانیان در شهری اسطوره‌ای به نام مسون (Mecone) درگیر می‌شوند.

پرومته که خدا و یکی از بزرگ‌ترین خیرخواهان بشر بود، برای اهدای قربانی و ساکت‌ کردن خدایان، یک گاو نر سلاخی‌شده را به دو بخش تقسیم کرد. یکی از آن‌ها حاوی استخوان‌های خالی غیرجذاب بود که با لایه‌ای از چربی درخشان پوشیده شده بود و دیگری دارای گوشت مطلوبی بود که زیر بخش نازیبای شکم مخفی شده بود. پرومته از زئوس دعوت کرد تا یکی از آن‌ها را بردارد. زئوس که با چربی درخشان وسوسه شده بود، استخوان‌ها را انتخاب کرد.

در روایت فوق، پرومته ساده‌ترین شکل مسئله‌ برش کیک را با حیله و استراتژی «من می‌برم، تو انتخاب کن» ارائه می‌کند. اما این استراتژی در جهت برابری و انصاف به کار می‌رود و باید رضایت طرفین را تضمین کند. خروجی هم نسبی است به گونه‌ای که هر بازیکن احساس کند به سهم عادلانه‌ای رسیده است. بنابراین برای دو بازیکن، یک بازیکن سهم خود را ۱٫۲ می‌داند در حالی که برای سه بازیکن، سهم به اندازه‌ی ۱٫۳ است. و برای مقدار دلخواه گیرندگان کیک، سهم عادلانه به این ترتیب برابر با 1/n خواهد بود. با این‌حال اگر کیک شکل یکسانی داشته باشد، تمام بخش‌ها هم‌اندازه خواهند بود. در شکل‌های زیر مسئله برش کیک بین دو نفر شرح داده شده است.

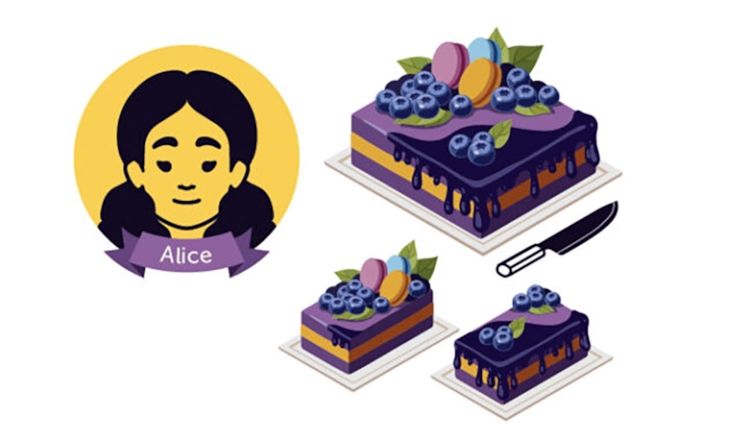
در ابتدا، شخص اول (آلیس) کیک را به دو قسمت عادلانه تقسیم می‌کند

شخص دوم (باب) برش دلخواه خود را انتخاب می‌کند و آلیس برش باقی‌مانده را برمی‌دارد. آلیس از این انتخاب رضایت دارد زیرا تصور می‌کند هر دو تکه عادلانه تقسیم شده‌اند. باب هم راضی است زیرا تکه‌ی موردعلاقه‌اش را انتخاب کرده است.

اما اگر کیک سراسر یکسان باشد، مسئله‌ی برش کیک از لحاظ ریاضی جذابیت چندانی نخواهد داشت. با روش تقسیم معمولی و ترازوی آشپزخانه به راحتی می‌توان یک کیک شکلاتی یکپارچه را به هر تعداد قسمت مساوی تقسیم کرد. مسئله‌ی برش کیک زمانی پیچیده می‌شود که کیک، شکلی ناهمگن داشته باشد. برای مثال دارای بخش‌هایی با طعم‌ها و تزئین‌های متغیر باشد.

حالا اگر شخصی عاشق گیلاس باشد، شاید کوچک‌ترین بخش با گیلاس دلخواهش را انتخاب کند. در این صورت اصطلاحا مسئله‌ی «مغایرت نیک‌بختی» مطرح می‌شود. همیشه ریاضیات زمانی جذاب می‌شود که دیدگاه‌های مخالف به میان می‌آیند. سناریوی دو نفره‌ی «من می‌برم، تو انتخاب کن» هنوز هم برای چنین مسئله‌ای صدق می‌کند. شخص تقسیم‌کننده، کیک را به دو بخش هم‌اندازه از دید خود تقسیم می‌کند. انتخاب‌کننده هم برش دلخواهش را انتخاب می‌کند. اما با افزایش تعداد گیرندگان کیک که هرکدام اولویت‌های خود را دارند، راه‌حل آسان خواهد بود.

هوگو استینهاوس از دانشگاه ورشو یکی از اولین ریاضیدان‌هایی بود که پیچیدگی‌های مسئله‌ی برش کیک را مطرح کرد. در طول جنگ جهانی دوم با مطرح شدن پرسش‌هایی مثل تقسیم عادلانه‌ی زمین در مقیاس‌های وسیع، استینهاوس استراتژی «من می‌برم، تو انتخاب کن» را برای سه بازیکن تعمیم داد. این روش «تقسیم‌کننده‌ی تنها» نامیده می‌شود.

در روش تقسیم‌کننده‌ی تنها، یک شخص که در اینجا به فرض آن را آلیس می‌نامیم، کیک را به سه بخش که به عقیده‌ی خود مساوی هستند، تقسیم می‌کند. هر تکه برابر با ۱٫۳ کل کیک است. دومین شخص یعنی باب، تکه‌ی دلخواه را انتخاب می‌کند. حالا دو تکه باقی می‌ماند، در اینجا شخص سوم به نام کارلا، تکه‌ی بعدی را انتخاب می‌کند و در نهایت آلیس هم تکه‌ی باقی‌مانده را برمی‌دارد.

با این‌حال اگر باب یا کارلا یک تکه‌ی یکسان را نخواهند، آن تکه کیک به آلیس می‌رسد. دو تکه‌ی باقی‌مانده که ارزش آن‌ها برابر با ۲٫۳ از کل است، دوباره ترکیب شده و با روش «من می‌برم تو انتخاب کن» بین باب و کارلا تقسیم می‌شوند. استینهاوس در سال ۱۹۴۸، این الگوریتم را در مقاله‌ای کوتاه با عنوان Econometrica توضیح می‌دهد. این مقاله یکی از دقیق‌ترین بررسی‌ها از مسئله‌ برش کیک است.

روش استینهاوس تنها برای سه نفر نتیجه‌بخش است، اما او در همان مقاله توضیح می‌دهد دو نفر از همکارانش این روش را برای تعداد دلخواه تعمیم داده‌اند. روش استینهاوس با عنوان «آخرین کاهنده» شناخته می‌شود و به این صورت است: شخص اول، تکه‌ای از کیک را که به نظر می‌رسد سهم منصفانه‌ای است، جدا می‌کند و آن تکه را به نفر بعدی می‌دهد.

بازیکنان باقی‌مانده این فرصت را دارند که بخشی از کیک را ببرند (اگر تصور کنند بیشتر از سهم برابر است) یا آن را به شخص دیگری بدهند (اگر فکر می‌کنند منصفانه یا کمتر منصفانه است). وقتی تمام اشخاص فرصت تقسیم یا کاهش یک برش را داشته باشند، آخرین شخصی که برش را انجام می‌دهد، تکه‌ی کیک را دریافت کرده و از بازی خارج می‌شود.

در نهایت تکه‌ی بریده شده مجددا با باقی‌مانده‌ی کیک ترکیب می‌شود و فرآیند فوق برای بازیکنان باقی‌مانده تکرار می‌شود. وقتی تنها دو بازیکن باقی ماندند، از استراتژی «من می‌برم تو انتخاب کن» استفاده می‌شود. در شکل‌های ذیل می‌توانید فرآیند روش «آخرین کاهنده» را ببینید.

در نوبت اول، اولین شخص (آلیس) یک تکه کیک را که به تصور او ۱٫۳ از مقدار کل کیک است، می‌برد و باقی‌مانده‌ی کیک را به شخص دوم (باب) می‌دهد.

اگر باب و شخص سوم (کارلا) تصور کنند قطعه‌ی بریده شده، بیشتر از ۱٫۳ کل کیک است، می‌توانند آن را به دلخواه ببرند یا در غیر این صورت به شخص بعدی بدهند. در این سناریو باب، تکه‌ای را که آلیس جدا کرده به کارلا می‌دهد و کارلا آن را می‌برد.

تکه به شخصی می‌رسد که آخرین برش را انجام داده. در این نمونه تکه‌ی کیک به کارلا می‌رسد. اگر باب و کارلا هر دو کیک را به نفر بعدی منتقل می‌کردند، آلیس تکه‌ی باقی‌مانده را دریافت می‌کرد.

در نوبت دوم، تمام برش‌ها به کیک باقی‌مانده اضافه می‌شوند و سپس، روش «تقسیم‌کننده، انتخاب‌کننده» برای دو نفر به کار می‌رود. آلیس کیک را به دو قسمت مساوی برش می‌زند.

باب هم برش دلخواهش را انتخاب می‌کند. و در نهایت آلیس برش باقی مانده را برمی‌دارد. همه نسبت به تکه‌ی کیک خود رضایت دارند. با این‌حال کارلا که زودتر از بازی خارج شده، هنوز تصور می‌کند تکه‌ی باب یا آلیس بهتر از تکه‌ی او است.

برامز، روش آخرین کاهنده را روشی برجسته می‌داند زیرا تضمین می‌کند هر شخصی تکه‌ای را که به زعم خود عادلانه می‌داند، انتخاب می‌کند، اما این روش بی‌نقص نیست زیرا مسئله‌ی حسادت را درنظر نمی‌گیرد. در هر دو روش آخرین کاهنده و تقسیم‌کننده‌ی تنها، شخصی که زودتر از بازی خارج می‌شود در نهایت به تکه‌ای طمع دارد که بعد از او در بازی تقسیم شده است. این در حالی رخ می‌دهد که آن شخص ممکن است در ابتدا سهم خود را منصفانه بداند.

محدودیت کاربردی دیگری برای روش آخرین کاهنده وجود دارد: با توجه به تعداد کافی بازیکن‌ها، کیکی که در نوبت‌های بعدی باقی می‌ماند به تعداد زیادی برش تقسیم شده یا حتی به خرده نان شباهت پیدا می‌کند. در نتیجه اشخاص بعدی ممکن است ارزشی برای این کیک قائل نشوند.

آیا برش کیک می‌تواند خالی از حسادت باشد؟

از زمان معرفی روش آخرین کاهنده، مسئله‌ی برش کیک توجه بخش مهمی از ریاضیدان‌ها را به خود جلب کرد.. در دهه‌ی ۱۹۶۰ گامی مهم در جهت این مسئله برداشته شد. جان کانوی و جان سفلریج به صورت مستقل از یکدیگر به الگوریتم جدید برش کیک برای سه نفر دست پیدا کردند. برخلاف کارهای استینهاوس و همکارانش، دستورالعمل جدید بدون حسادت و به صورت منصفانه کیک را بین دریافت‌کنندگان تقسیم می‌کرد.

به عقیده‌ی هریس عزیز، پژوهشگر ریاضی، دستیابی به راه‌حل بدون حسادت که در آن هیچ طعمی بر تکه‌ی دیگری وجود نداشته باشد، کار آسانی است. بر اساس راه‌حل آسان اگر کیک را کنار بگذارید و هیچ تکه‌ای را بین افراد تقسیم نکنید، کسی هم برای حسادت وجود نخواهد داشت.

بااین حال اگر کیک سر از سطل زباله دربیاورد، کسی خوشحال نخواهد بود. در طرح رضایت‌بخش‌تر کانوی و سلفریج، آلیس در ابتدا کیک را به سه قسمت که به باور او برابر هستند، تقسیم می‌کند. سپس باب دوباره یکی از تکه‌ها را به دلخواه تقسیم می‌کند. کیک‌های برش خورده کنار گذشته می‌شوند. حالا کارلا از میان سه تکه‌ای که آلیس تقسیم کرده، انتخاب می‌کند. سپس ترتیب برعکس می‌شود و اگر کارلا تکه‌ای را که باب برش زده انتخاب نکند، باب آن را برمی‌دارد. در نهایت آلیس تکه‌ی باقی‌مانده را برمی‌دارد. سپس گیرنده‌ها به سمت تکه‌هایی که مجددا برش خورده‌اند رو می‌آورند و این پروتکل تکراری تقسیم، برش و انتخاب ادامه پیدا می‌کند.

در نوبت اول، شخص اول (آلیس)، کیک را به سه قسمت که به باور او برابر هستند، تقسیم می‌کند.

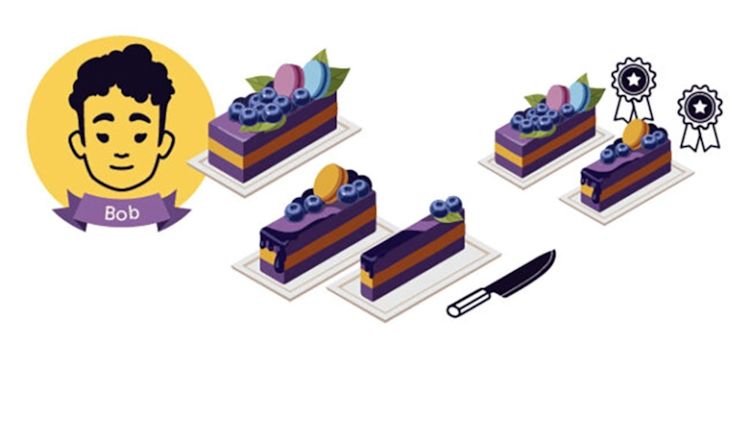
شخص دوم (باب) یا می‌تواند یکی از قسمت‌ها را مجددا برش بزند یا آن را به نفر بعدی بدهد. تکه‌های برش‌خورده کنار گذاشته می‌شوند.

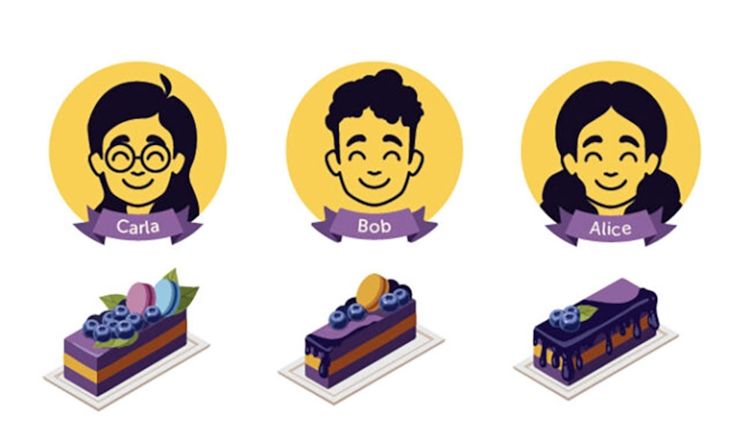
شخص سوم (کارلا)، در ابتدا یکی از تکه‌های تقسیم‌شده توسط آلیس را برمی‌دارد که مورد علاقه‌ی اوست. سپس باب تکه‌اش را برمی‌دارد (در صورتی که کارلا قطعه‌ی برش خورده را برندارد، باب آن را انتخاب می‌کند). آلیس قطعه‌ی باقی‌مانده، یعنی یکی از تکه‌هایی را که در ابتدا تقسیم کرده بود، انتخاب می‌کند.

در نوبت دوم، تکه‌های برش‌خورده مجددا تقسیم می‌شوند. هر شخصی (باب یا کارلا) قطعه‌ی بریده نشده را انتخاب کند (در این نمونه کارلا)، قطعه‌ی بریده‌شده را به سه قسمت با ارزش‌های برابر تقسیم می‌کند.

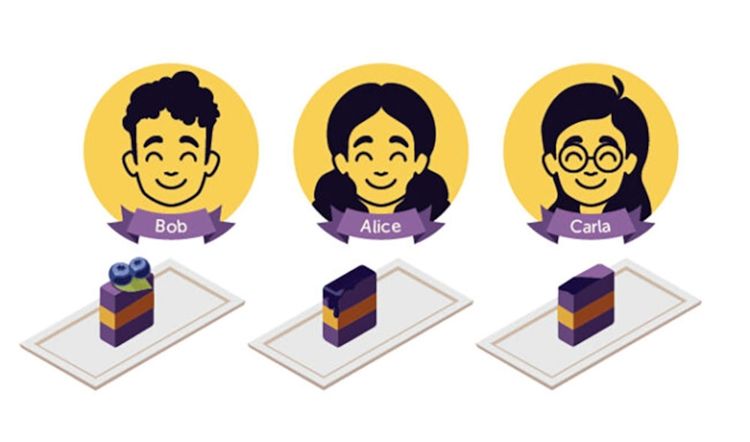
باب اول انتخاب می‌کند و تکه دلخواه را برمی‌دارد. آلیس که تصور می‌کرد تکه‌ی خودش بهتر از تکه‌ی برش‌خورده در نوبت قبل بود، تکه‌ی بعدی را برمی‌دارد. در نهایت یکی از تکه‌های برش‌خورده هم برای کارلا باقی می‌ماند. این روش بدون حسادت است زیرا باب در ابتدا تکه‌اش را برمی‌دارد، از طرفی کارلا تمام برش‌ها را برابر ارزیابی می‌کند و آلیس هم هر برش را مانند یک امتیاز می‌بیند چرا که نسبت به تکه‌ی اصلی خود که در ابتدای کار از کیک جدا کرده بود، رضایت دارد.

با این‌حال به مدت چنددهه، راه‌حل برش کیک بدون حسادت برای تعداد دلخواه گیرندگان گیج‌کننده بود. در اواخر دهه‌ی ۱۹۸۰، ریاضیدانی به نام سال گارفونکل در برنامه‌ی تلویزیونی خود با عنوان «برای تمام اهداف کاربردی: مقدمه‌ای بر ریاضیات معاصر»، مسئله‌ی حل‌نشده‌ی برش کیک و پرسش‌های مرتبط با تقسیم عادلانه را مطرح کرد.

مسئله‌ی برش کیک در نهایت بدون راه‌حل باقی نماند. در سال ۱۹۹۵، برامز و آلن دی تایلور، رویه‌ای جدید را ابداع کردند که کیک را برای چهار نفر تقسیم می‌کند، به‌طوری که هیچ شخصی به سهم دیگری حسادت نکند. این روش هم مبتنی بر روش بریدن تکه‌های کانوی و سلفریج بنا شد و رویه‌ی مشابهی را برای تمام زوج‌های احتمالی گیرندگان کیک اعمال کرد. برامز و تایلور چگونگی تعمیم رویه به تعداد دلخواه افراد را توضیح دادند.

با این‌حال روش فوق هم محدودیت‌هایی داشت. برای مثال، هیچ تضمینی وجود نداشت که تعداد برش‌های لازم چقدر باید باشد. در واقع آن‌ها در حالت کلی نشان دادند که تعداد برش‌ها می‌تواند بین ۳ تا ۳ میلیون عدد باشد.

چندسال‌ بعد ریاضیدان‌هایی به نام جک رابرتسون و ویلیام وب از دانشگاه ایالتی واشنگتن در پولمن، مدل محاسباتی سودمندی را توصیف کردند که می‌توان از آن برای تحلیل تعداد گام‌ها به ویژه تعداد برش‌ها و ارزیابی‌های لازم در یک الگوریتم استفاده کرد. این محاسبات ثابت کردند هیچ تعداد حداکثر برشی را نمی‌توان برای الگوریتم‌های شناخته‌شده در آن زمان پیش‌بینی کرد که بتوانند کیک را با تکه‌های برابر و بدون برانگیختن حسادت برای تعداد دلخواه بازیکنان تقسیم کنند.

در طی چند دهه‌ی بعد، تعداد زیادی از ریاضیدان‌ها به جستجوی کران بالای مسئله‌ی برش کیک بدون حسادت پرداختند. در صورت عدم پیدا شدن راه‌حل، این مسئله می‌توانست تا ابد ادامه پیدا کند. علاوه بر این به گفته‌ی پروکاچیا هیچ‌کس حداقل برش‌ها را محاسبه نکرده بود.

آیا مسئله بریدن کیک نامتناهی است؟

پروکاچیا هرگز وقت خود را صرفا متمرکز بر مسئله برش کیک نکرد. در واقع او در سال ۲۰۰۸ واحدی به نام مبانی ریاضیات هوش مصنوعی را تدریس می‌کرد. یک روز پس از ارائه‌ی سخنرانی درباره‌ی تخصیص منابع و مدل رابرتسون، وب، متوجه شد می‌تواند کران پائینی (حداقل تعداد برش‌ها) را برای بریدن کیک بدون حسادت برای تعداد دلخواه از افراد پیدا کند. کران پائینی تقریبا برابر با n2 برش بود که در آن n برابر است با تعداد گیرندگان کیک.

به این ترتیب پروکاچیا اولین مقاله‌ی خود را درباره‌ی کیک نوشت. او همچنین مهارت خاصی در انتخاب عنوان‌های جذاب برای مقاله‌های ریاضی داشت. مقاله‌ی کران پائین در سال ۲۰۰۹ با عنوان «تو باید به کیک همسایه طعم کنی» منتشر شد. در سال ۲۰۱۰ او در مقاله‌ای با عنوان «حقیقت، انصاف و بریدن کیک» همکاری کرد که مسئله‌ی حق‌گویی را مطرح می‌کرد و در عین حال تناسب و حذف حسود را تضمین می‌کرد. در صورتی که شخصی اولویت‌های خود را در طول بریدن کیک مخفی کند، این احتمال وجود دارد که به سهمی نابرابر برسد.

مسئله‌ی بریدن کیک این پرسش را مطرح می‌کند: چه روشی برای بریدن کیک تضمین می‌کند که همه نسبت به نتیجه راضی هستند؟

پروکاچیا با ادامه‌ی پژوهش‌ها درباره‌ی الگوریتم‌های مفیدی فکر کرد که از دیدگاه‌های برش کیک و به‌طورکلی مسئله‌ی تقسیم عادلانه استفاده می‌کنند. یکی از این مسئله‌ها تقسیم اجاره بود. ساده‌ترین روش، تقسیم کل اجاره بر تعداد ساکنین بود، اما این مسئله «مغایرت نیک‌بختی» را نادیده می‌گیرد. برای مثال شخصی پنجره می‌خواهد و شخصی دیگر کمد بزرگ‌تر را ترجیح می‌دهد. در سال ۲۰۱۴، پروکاچیا و همکاران او ابزار مبتنی بر وبی به نام Spliddit را طراحی کردند که اولویت‌های کاربرها را جمع‌آوری می‌کرد و روش‌های منصفانه‌ی ریاضی را برای تقسیم هرچیزی از اجاره‌خانه گرفته تا دارایی‌ها در میان طرفین طلاق را ارائه می‌داد.

مسئله برش کیک را می‌توان در نمونه‌های کاربردی مثل تخصیص غذا و مناطق رأی‌گیری به کار برد

هریس عزیز و سیمون مکنزی، دانشمندان کامپیوتر به یکی از بزرگ‌ترین پیشرفت‌ها در حل مسئله‌ی بریدن کیک رسیدند. این دو نفر، کران بالایی را برای مسئله‌ی برش کیک متناسب بدون حسادت مطرح کردند. در درجه‌ی اول این دو پژوهشگر مسئله‌ی اشتراک‌گذاری کیک بین چهار نفر را حل کردند. این گروه با قرض گرفتن ایده‌های کانوی و سلفریج و برامز و تایلر، الگوریتمی را ابداع کردند که کران بالای ۲۰۳ گام را تولید می‌کند که تقریبا می‌تواند شامل تعداد زیادی برش شود. قطعا این مقدار زیاد منطقی نیست.

یک سال بعد، گروه پژوهشگرها روشی را برای تعداد دلخواه افراد توسعه دادند و الگوریتمی با تعداد متناهی برش‌ها برای بریدن کیک بدون حسادت ارائه دادند. این الگوریتم هم به عددی نجومی برای برش‌ها رسید، اما متناهی بود و به پرسشی دیرینه در این زمینه پاسخ می‌داد.

مسئله‌ی بریدن کیک برای n نفر، ممکن است به n^n^n^n^n^n عملیات نیاز داشته باشد. این تعداد کاملا غیرمنطقی است. حداکثر تعداد گام‌ها برای پنج نفر می‌تواند تقریبا برابر با 2 x 102,180 باشد. بااین‌حال به گفته‌ی عزیز، می‌توان شکل منطقی‌تری به این الگوریتم داد و ریاضی‌دان‌ها در آینده می‌توانند کران بالا را کاهش دهند.

مسئله بریدن کیک همچنان ادامه دارد

بررسی‌های تقسیم عادلانه کیک به پایان نرسیده‌اند. بیائوشای تائو از دانشگاه شانگهای با الهام از مقاله‌ی پروکاچیا به بررسی این مسئله پرداخت: چه اتفاقی رخ می‌دهد وقتی بخواهید عدم صداقت را برای گیرندگان کیک درنظر بگیرید؟

با این‌حال در برخی نمونه‌ها، عدم صداقت می‌تواند به مزیت بینجامد. اگر آلیس و باب، کیک را تقسیم می‌کردند و آلیس می‌دانست که باب همیشه شکلات را ترجیح می‌دهد، احتمالا آگاهانه کیک را به شکل نابرابر تقسیم می‌کرد، به‌طوری‌که بخش کوچک‌تر حاوی شکلات بیشتری باشد. سپس باب، انتخاب را بر اساس اولویت خود انجام می‌داد و آلیس هم تکه‌ی بزرگ‌تر را دریافت می‌کرد.

تائو در پژوهشی دیگر در سال ۲۰۲۲ به این نتیجه رسید که حقیقت و تناسب در واقع ناسازگار هستند و همین مسئله ساخت الگوریتم برش کیکی را که حقیقت‌گویی، تناسب و عدم حسادت را تضمین کند، غیرممکن می‌سازد.

کاربردهای عملی مسئله‌ی برش کیک هم همچنان ادامه دارند. منطقه‌ای با صندلی‌های محدود در برخی مدرسه‌ها باید بر اساس اولویت‌ها تنظیم شود. از این اولویت‌ها می‌توان به امتحان‌های ورودی یا توزیع جغرافیایی اشاره کرد. این متعادل‌سازی باید به گونه‌ای باشد که والدین بتوانند یک راه‌حل متناسب را با یک مقدار عادلانه پیدا کنند. در گذشته مدرسه‌ها بدون پرسیدن اولویت افراد، انتخاب می‌شدند، اما امروز باید اولویت والدین و فرزندانشان را هم در نظر گرفت.

به‌طورکلی تعداد زیادی از کاربردهای واقعی برای پرسش‌های تقسیم عادلانه وجود دارند. برامز از ایده‌های بریدن کیک برای بررسی رویه‌های رأی‌گیری عادلانه استفاده کرده است. پروکاچیا هم الگوریتم‌های تقسیم عادلانه را برای مدلسازی تخصیص غذایی به کار برد. از طرفی عزیز، در حال بررسی کاربردهای مثل تقسیم کارهای روزمره تا وظایف‌ دیگری مثل بهترین زمان‌بندی شیفت پزشکان در بیمارستان است.

برخی پژوهشگرها هم روی تخصیص منابعی کار می‌کنند که به‌صورت دقیق تقسیم‌پذیر نیستند. برای مثال زوج‌ها پس از طلاق احتمالا به توافقی مبنی بر تقسیم عادلانه‌ی اموال برسند. این بررسی‌ها شامل روش‌هایی نزدیک به روش بدون حسادت هستند و شاید از لحاظ ریاضی بی‌نقص نباشند.

مسئله‌ی بریدن کیک حتی پس از سال‌ها بررسی مانند یک پازل جورچینی ساده با یک راه‌حل تعریف‌شده نیست. بلکه به‌مرورزمان به گونه‌ای به تکامل رسیده است که اثبات‌های و کاربردهای شهودی را گرد هم می‌آورد. هرچقدر پژوهشگرها در این زمینه جستجو کنند، به نکات بیشتری برای جستجو خواهند رسید.